ГЕДЕЛЬ, ЭШЕР, БАХ: эта бесконечная гирлянда.

ГЛАВА XIII: Блуп, Флуп и Глуп.

Самосознание и хаос.

Блуп, Флуп и Глуп — это не имена гномов, не разговоры лягушек в пруду и не бульканье воды в засорившейся раковине. Это компьютерные языки, каждый из которых имеет особое предназначение. Они были придуманы специально для этой главы. Мы воспользуемся ими для того, чтобы объяснить новые значения слова «рекурсивный» — в частности, понятия примитивной рекурсивности и общей рекурсивности. Эти понятия помогут нам лучше объяснить механизм автореферентности в ТТЧ.

Здесь мы совершаем скачок от человеческого мозга и интеллекта к миру математики, техники и компьютеров. Этот переход, каким бы резким он не казался, все же имеет смысл. Мы только что убедились в том, что в сердце интеллекта лежит самосознание. Давайте теперь рассмотрим «самосознание» в более формальных контекстах, таких, как ТТЧ. Между ТТЧ и разумом — огромная дистанция; тем не менее, некоторые идеи окажутся весьма поучительными и, может быть, даже приложимыми к нашим рассуждениям о сознании.

Удивительно то, что самосознание в ТТЧ тесно связано с вопросом о порядке и хаосе среди натуральных чисел. В частности, мы увидим, что упорядоченная система, достаточно сложная, чтобы отразить саму себя, не может быть полностью упорядоченной — в ней обязательно окажутся некие странные, хаотические черты. Читателям, в которых есть что-то от Ахилла, трудно будет в это поверить. Однако здесь существует и некая «магическая» компенсация, что-то вроде порядка внутри хаоса; этот «хаотический порядок» изучается так называемой «теорией о рекурсивных функциях». К несчастью, здесь мы сможем дать только самое поверхностное понятие об этой интереснейшей теме.

Представимость и холодильники.

Мы с вами уже довольно часто натыкались на такие выражения, как «достаточно сложный», «достаточно мощный» и тому подобное. Что именно они означают? Давайте вернемся к «войне» Краба с Черепахой и подумаем, какие качества необходимы предмету, чтобы его можно было бы назвать патефоном? Почему бы Крабу не сказать, что его холодильник — это «совершенный» патефон? В доказательство он мог бы положить на холодильник любую пластинку и сказать: «Вот видите, он ее проигрывает!» Если бы Черепаха захотела что-то противопоставить этому дзен-буддйстскому акту, она должна была ответить: «Нет, ваш холодильник такого низкого качества, что его нельзя назвать патефоном: он вообще не может воспроизводить звуков (а тем более, саморазбивальных звуков)». Черепаха может записать пластинку под названием «Меня нельзя сыграть на патефоне X», только если патефон X действительно является патефоном! Метод Черепахи весьма хитер, так как он играет не на слабости системы, а на ее силе. Поэтому, чтобы он подействовал, необходимы патефоны достаточно высокого качества.

То же самое верно и для формальных вариантов теории чисел. ТТЧ является формализацией теории чисел (Ч) именно потому, что ее символы действуют «так как надо»: они не молчат, как холодильник, а выражают существующие в теории чисел истины. Конечно, так же ведут себя символы системы pr. Можно ли и эту систему считать за формализацию Ч, или же она больше похожа на холодильник? На самом деле, она чуть получше холодильника, но все еще очень слаба. Система pr не включает достаточного количества основных истин Ч и поэтому не может считаться за «теорию чисел».

Что же такое «основные истины» Ч? Это примитивно рекурсивные истины, что означает, что они включают только предсказуемо конечные вычисления. Эти основные истины являются для Ч тем же, чем четыре постулата Эвклида для геометрии: они позволяют нам забраковать некоторых кандидатов еще до начала игры, на основании того, что они «недостаточно мощные». В дальнейшем, критерием «достаточной мощности» системы будет представимость в ней всех примитивно рекурсивных истин.

Топор Ганто в метаматематике.

Важность этого понятия видна из следующего факта; если у вас есть достаточно мощная формализация теории чисел, то к ней приложим метод Гёделя — следовательно, ваша система неполна. С другой стороны, если ваша система недостаточно мощна (то есть, если не все примитивно рекурсивные истины являются ее теоремами), то она, именно в силу этого недостатка, все равно является неполной. Здесь перед нами тот же «Гантов топор», перенесенный в метаматематику: что бы система не делала, Гёделев Топор отсечет ее голову! Заметьте, что это положение дел также напоминает спор о высоком и низком качестве патефонов в «Акростиконтрапунктусе».

На самом деле оказывается, что метод Гёделя приложим даже к намного более слабым системам: критерий мощности, по которому все примитивно рекурсивные истины должны быть теоремами системы, оказывается слишком строгим. Это похоже на вора, который грабит только «достаточно богатых» людей — его жертва должна иметь в кармане по меньшей мере миллион долларов. К счастью, в случае ТТЧ, мы сможем стать такими грабителями, так как миллион у нее есть — иными словами, ТТЧ действительно содержит все примитивно рекурсивные истины в виде теорем.

Прежде чем углубиться в подробное обсуждение примитивно рекурсивных функций и предикатов, я постараюсь связать эту тему с темами предыдущих глав, чтобы дать читателю определенную перспективу.

Как обнаружить порядок с помощью правильного фильтра.

Мы уже с самого начала столкнулись с тем, что формальные системы могут вести себя как неукротимые и опасные бестии, когда в них есть удлиняющие и укорачивающие правила, поскольку это может привести к бесконечному поиску среди строчек. Открытие Гёделевой нумерации показало, что у любого поиска строчки с определенным типографским свойством есть арифметический кузен: изоморфный поиск целого числа с соответствующим арифметическим свойством. Следовательно, чтобы найти разрешающий алгоритм для формальных систем, необходимо решить проблему непредсказуемо длинного поиска — хаоса — среди строчек. Возможно, что в «Арии с различными вариациями» я преувеличил хаос в задачах о целых числах. В действительности, математикам удалось укротить гораздо худшие случаи кажущегося хаоса, чем проблема «интересности»; в конце концов, все они оказались довольно милыми зверями. Нерушимая вера Ахилла в регулярность и предсказуемость чисел достойна немалого уважения по крайней мере потому, что она отражает взгляды, которых придерживались почти все математики до 1930-х годов. Чтобы показать, почему противопоставление порядка и хаоса такая деликатная и важная тема, и связать ее с вопросом о местоположении и извлечении значения, я хотел бы процитировать здесь замечательный и памятный отрывок из диалога «Реальны ли числа?» написанного в Галилеевом стиле покойным Ж. М. Джочем (J.M. Jauch. Are quanta real?):

Джоч говорит здесь о «сообщениях», посланных не разумными существами, но самой природой. Однако вопрос об отношении смысла и сообщения, на который мы пытались ответить в главе VI, может быть задан и здесь. Хаотична ли природа, или же в ней имеется некая закономерность? И какова роль интеллекта в поисках ответа на этот вопрос?

Теперь оставим в стороне философию и подумаем над вопросом регулярности рядов, выглядящих хаотическими. Может ли быть; что у функции Q(n) из главы V есть также и простое, нерекурсивное объяснение? Можно ли увидеть любую проблему, как фруктовый сад, с такого угла, что ее секрет становится явным? Или же в теории чисел есть проблемы, остающиеся загадкой, с какого бы угла мы их не рассматривали?

После этого вступления мне кажется, что настало время точно определить термин «предсказуемо длинный поиск». Для этого мы воспользуемся языком БЛУП.

Основные шаги в языке Блуп.

Мы займемся здесь поисками натуральных чисел с различными свойствами. Чтобы мы могли говорить о длине поиска, нам необходимо определить некие основные шаги, из которых состоит каждый поиск. Тогда мы сможем измерять длину поиска количеством шагов. Вот некоторые шаги, которые можно считать основными:

Сложение двух натуральных чисел;

Умножение двух натуральных чисел;

Определение равенства двух чисел;

Определение того, какое из двух чисел больше.

Петли и верхние границы.

Если мы попытаемся сформулировать некий тест, — например, на простоту чисел, — в терминах таких шагов, мы вскоре увидим, что нам необходимо включить в него управляющую структуру — описание того, в каком порядке надо действовать: когда надо отойти назад и попытаться сделать что-то снова, или пропустить несколько шагов, или остановиться и т. п.

Любой алгоритм — описание того, как выполнить определенное задание — обыкновенно состоит из смеси (1) набора конкретных операций и (2) контрольных высказываний. Таким образом, разрабатывая наш язык для описания предсказуемо длинных вычислений, мы должны включить в него также основные контрольные структуры. Отличительное свойство Блупа — это ограниченное количество его контрольных структур. В нем нельзя совершать произвольные шаги или повторять группы шагов до бесконечности. Практически единственная контрольная структура Блупа — это ограниченные петли: набор команд, которые можно повторять снова и снова, но лишь ограниченное число раз; это число называется верхней границей, или потолком петли. Если потолок данной петли 300, то она может быть выполнена 0,7 или 300 раз — но не 301.

Программист не должен вводить в программу точной величины всех верхних границ; в действительности, он может и не знать этого заранее. Вместо этого, каждый потолок может быть вычислен до того, как программа начинает выполнять соответствующую петлю. Например, если вы собираетесь вычислить величину 2 ^{3 n}, у вас будут две петли. Сначала вы подсчитаете 3 ⁿ; для этого вам придется применить умножение n раз. Затем вы возьмете полученное число и возведете два в эту степень. Таким образом, верхняя граница второй петли — результат вычислений, произведенных вами в первой петле.

В программе Блуп это выражается следующим образом:

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «ДВА-В-СТЕПЕНИ-ТРИ-В-СТЕПЕНИ»[N]:

БЛОК 0:НАЧАЛО.

ЯЧЕЙКА(О)<=1;

ЦИКЛ N РАЗ;

БЛОК 1: НАЧАЛО.

ЯЧЕЙКА(О)<= 3 * ЯЧЕЙКА(О);

БЛОК 1:КОНЕЦ;

ЯЧЕЙКА(1) <= 1;

ЦИКЛ ЯЧЕЙКА(О) РАЗ:

БЛОК 2:НАЧАЛО.

ЯЧЕЙКА(1)<= 2 * ЯЧЕЙКА(1);

БЛОК 2:КОНЕЦ;

ВЫХОД <= ЯЧЕЙКА(1);

БЛОК 0:КОНЕЦ.

Условности языка Блуп.

Умение читать программу, написанную на компьютерном языке, и понимать, что она делает, приходит со временем. Но надеюсь, что этот алгоритм достаточно прост, чтобы его можно было понять без особого труда. В нем определяется процедура, имеющая одно входное значение — N; выходом этой процедуры будет искомая величина.

Данное определение процедуры имеет блочную структуру; это означает, что некоторые его порции должны рассматриваться как единицы, или блоки. Все действия в блоке выполняются как одно целое. Каждый блок пронумерован (внешний блок получает номер 0) и ограничен НАЧАЛОМ и КОНЦОМ. В нашем примере в БЛОКЕ 1 и БЛОКЕ 2 было всего по одной инструкции, но вскоре мы будем иметь дело с более длинными блоками. Инструкция ЦИКЛ означает, что нужно повторить несколько раз блок, следующий ниже. Как вы видели выше, блоки могут быть вставлены один в другой.

Стратегия этого алгоритма ничем не отличается от той, которую я описал выше. Сначала вы берете вспомогательную переменную под названием ЯЧЕЙКА(0); для начала, вы придаете ей значение 1 и затем, исполняя цикл, вы несколько умножаете ее на 3 и повторяете это ровно N раз. Потом вы повторяете ту же процедуру для ЯЧЕЙКИ(1): придаете ей значение 1 и умножаете на 2 ровно ЯЧЕЙКА(0) раз; после этого вы останавливаетесь. Наконец, вы придаете выходу значение, полученное вами для ЯЧЕЙКИ(1). Именно эта величина достигает внешнего мира — это единственное действие процедуры, заметное извне.

Необходимо отметить кое-что относительно нотации. Прежде всего, значение указывающей налево стрелки следующее:

Вычислить выражение справа, взять результат и придать это значение ЯЧЕЙКЕ (или ВЫХОДУ) слева.

Таким образом, команда ЯЧЕЙКА(1) <= 3 * ЯЧЕЙКА(1) означает что вы должны утроить величину ЯЧЕЙКИ(1). Каждую ЯЧЕЙКУ можно представить как отдельное слово в памяти компьютера. Единственная разница между ЯЧЕЙКОЙ и настоящим словом заключается в том, что последнее может содержать только целые числа до определенного конечного предела, в то время как в ЯЧЕЙКЕ может храниться сколь угодно большое натуральное число.

Каждая процедура в Блупе, будучи вызванной, производит определенную величину — а именно, величину переменной под названием ВЫХОД. В начале выполнения любой процедуры мы предполагаем, что при отсутствии дополнительных указаний ВЫХОДОМ будет 0. (Подобное предположение называется выбором по умолчанию, или стандартным выбором.) Благодаря этому, даже если процедура не установит никакого иного ВЫХОДА, мы тем не менее всегда будем знать его величину.

Команды ЕСЛИ и разветвление.

Давайте теперь посмотрим на другую процедуру, которая покажет нам некоторые черты Блупа, делающие эту программу более общей. Каким образом можно найти значение M-N, если мы умеем только складывать? Трюк состоит в том, чтобы прибавлять различные числа к N до тех пор, пока мы не получим таким образом М. Но что, если М меньше N? Что, если нам нужно отнять 5 от 2? В области натуральных чисел ответа на этот вопрос нет. Но мы хотим, чтобы наша процедура Блуп все равно дала бы нам ответ — скажем, 0. Вот процедура Блупа, которая выполняет вычитание:

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «ВЫЧИТАНИЕ»[M,N]:

БЛОК 0: НАЧАЛО.

ЕСЛИ M < N, ТО;

ВЫЙТИ ИЗ БЛОКА 0;

ПОВТОРИТЬ ЦИКЛ НЕ БОЛЬШЕ ЧЕМ M + 1 РАЗ;

БЛОК 1:НАЧАЛО.

ЕСЛИ ВЫХОД + N = M, ТО:

ПРЕРВАТЬ ЦИКЛ 1;

ВЫХОД <= ВЫХОД + 1;

БЛОК 1:КОНЕЦ;

БЛОК 0:КОНЕЦ.

Здесь мы предполагаем, что ВЫХОД начинается с нуля. Если М меньше N, то вычитание становится невозможным, и мы сразу перескакиваем к БЛОКУ 0; в таком случае, ответ равняется 0. Именно это означает строчка ВЫЙТИ ИЗ БЛОКА 0. Но если М не меньше N, то мы пропускаем эту строчку и выполняем следующую команду (здесь это повторение цикла). Так работают в Блупе команды типа ЕСЛИ.

Итак, мы входим в ЦИКЛ 1, называющийся так потому, что он предлагает нам повторить БЛОК 1. Мы пробуем добавить к N сначала 0, затем 1, 2 и т. д., пока не находим числа, дающего в результате М. В этот момент мы ПРЕРЫВАЕМ цикл, в котором мы находимся, то есть переходим к команде, сразу следующей за КОНЦОМ этого цикла. В данном случае, мы попадаем к команде БЛОК 1: КОНЕЦ. Это последняя команда нашего алгоритма. ВЫХОД теперь содержит правильный ответ.

Заметьте, что у нас есть две различных команды, позволяющие нам перепрыгнуть вниз: ВЫЙТИ и ПРЕРВАТЬ. Первая относится к блокам, вторая — к циклам. ВЫЙТИ ИЗ БЛОКА н означает перейти к его последней строчке, в то время как ПРЕРВАТЬ ЦИКЛ н значит перепрыгнуть к строчке, сразу следующей за последней строчкой БЛОКА N. Это различие важно только тогда, когда вы находитесь внутри цикла и хотите его продолжить — но при этом хотите выйти из соответствующего блока; это исполняет команда ВЫЙТИ.

Заметьте также, что слова НЕ БОЛЬШЕ ЧЕМ теперь находятся перед верхней границей цикла; это говорит нам, что цикл может быть прерван до того, как достигнута его верхняя граница.

Автоматическое создание блоков.

Остается объяснить две важные особенности Блупа. Первая из них состоит в том, что однажды определенная процедура может быть вызвана при определении следующих процедур. Она рассматривается в таком случае как нечто целое, как основной шаг. Эту черту Блупа можно назвать автоматическим созданием блоков. Это сравнимо с тем, как хороший фигурист выучивает новые движения: вместо длинной последовательности основных мускульных действий, он повторяет ранее выученные движения, которые, в свою очередь, состоят из ранее выученных движений — и так далее. Возможно, что нам придется отступить на несколько уровней, пока мы не придем к уровню «основных мускульных действий». Так же, как репертуар движений фигуриста, репертуар петель и прыжков Блупа растет очень быстро.

Тесты в Блупе.

Другая важная черта Блупа — это то, что выходом некоторых процедур в нем может быть ДА или НЕТ вместо числового значения. Такие процедуры являются не функциями, но тестами. Чтобы указать на эту разницу, в конце названия теста ставится вопросительный знак. Кроме того, стандартным выбором ВЫХОДА здесь, разумеется, будет не 0, а НЕТ.

Давайте посмотрим, как работают эти черты Блупа в алгоритме, проверяющем, какие числа являются простыми.

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «ПРОСТОЕ?» [N]:

БЛОК 0:НАЧАЛО.

ЕСЛИ N = О, ТО:

ВЫЙТИ ИЗ БЛОКА 0;

ЯЧЕЙКА(0) <= 2;

ПОВТОРИТЬ ЦИКЛ НЕ БОЛЕЕ ЧЕМ МИНУС [N,2] РАЗ:

БЛОК 1: НАЧАЛО.

ЕСЛИ ОСТАТОК [N, ЯЧЕЙКА(0)] = 0, ТО;

ВЫЙТИ ИЗ БЛОКА 0;

ЯЧЕЙКА(0)<= ЯЧЕЙКА(0) +1;

БЛОК 1: КОНЕЦ;

ВЫХОД <= ДА;

БЛОК 0: КОНЕЦ.

Заметьте, что в этом алгоритме я вызвал две процедуры: МИНУС и ОСТАТОК. (Имеется в виду, что последняя была определена раньше; вы можете попробовать найти ее определение сами.) Этот тест на простоту чисел работает, перебирая один за другим потенциальные множители N, начиная с двух и кончая не более чем N-1. Если при делении N на любое из этих чисел остаток равняется нулю, то мы перескакиваем к концу алгоритма, поскольку на этой стадии ВЫХОД еще стандартный — НЕТ. Только если N не делится ни на одно из этих чисел, оно сможет пройти весь ЦИКЛ 1; тогда мы придем к команде ВЫХОД <= ДА, и после ее выполнения процедура будет закончена.

Программы Блупа содержат цепи процедур.

Мы только что видели, как определяются процедуры в Блупе; однако, определение процедуры — лишь часть программы. Программа состоит из цепи определений процедур, каждая из которых вызывает определенные ранее процедуры. За этим может следовать один или несколько вызовов определенных таким образом процедур. Таким образом, примером полной программы Блупа было бы определение процедуры ДВА В СТЕПЕНИ ТРИ В СТЕПЕНИ, с последующим вызовом.

ДВА В СТЕПЕНИ ТРИ В СТЕПЕНИ [2].

Результатом чего было бы 512.

Если у вас есть только цепь определений процедур, то ни одна из них не исполняется; для этого необходим некий вызов, вводящий специфические числовые величины. Только тогда процедуры начинают действовать. Это напоминает мясорубку, ждущую, чтобы в нее заложили порцию мяса — или, скорее, целую цепь мясорубок, связанных таким образом, что каждая из них получает сырье от предыдущих. Сравнение с мясорубками, возможно, не слишком аппетитно; однако в случае программ Блупа это понятие очень важно. Такие программы мы будем называть «программами без вызова». Пример подобной программы показан на рис. 72.

Блуп — язык для определения предсказуемо конечных вычислений. Стандартное название функций, которые можно просчитать на Блупе, — примитивно-рекурсивные функции; стандартное название свойств, которые можно обнаружить с помощью тестов на Блупе, — примитивно-рекурсивные предикаты. Так, функция 2³ⁿ — примитивно-рекурсивная функция, а утверждение «n — простое число» — примитивно-рекурсивный предикат.

Интуиция подсказывает нам, что свойство Гольдбаха — примитивно-рекурсивное; чтобы сделать это яснее, я приведу определение процедуры Блупа, которая показывает, как можно проверить наличие или отсутствие этого свойства:

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «ГОЛЬДБАХ?» [N]:

БЛОК 0: НАЧАЛО.

ЯЧЕЙКА(О) <= 2;

ПОВТОРИТЬ ЦИКЛ НЕ БОЛЬШЕ N РАЗ;

БЛОК 1: НАЧАЛО.

ЕСЛИ {ПРОСТОЕ? [ЯЧЕЙКА(О)].

И ПРОСТОЕ? [МИНУС [N, ЯЧЕЙКА(0)]]},

ТОГДА:

БЛОК 2:НАЧАЛО.

ВЫХОД 2: <= ДА;

ВЫЙТИ ИЗ БЛОКА 0;

БЛОК 2: КОНЕЦ.

ЯЧЕЙКА(0) <= ЯЧЕЙКА(0) + 1;

БЛОК 1:КОНЕЦ;

БЛОК 0: КОНЕЦ.

Как обычно, мы предполагаем, что выходом будет НЕТ, если не доказано обратное, и мы просто ищем при помощи «грубой силы» такие пары чисел, которые в сумме дают N. Если они оба — простые числа, то мы выходим из внешнего блока; в противном случае, мы пробуем снова, пока не исчерпаем все возможности.

(Внимание: тот факт, что свойство Гольдбаха — примитивно-рекурсивное, не означает, что вопрос «все ли числа обладают свойством Гольдбаха» прост. Это далеко не так!).

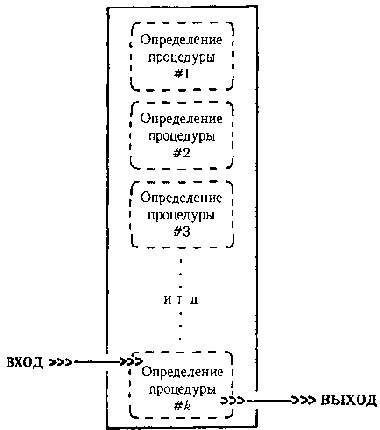
Рис. 72. Структура программы без вызова в Блупе. Чтобы такая программа была самодостаточная, каждое определение процедуры может вызывать только те процедуры, определенные выше него.

Предлагаемые упражнения.

Сможете ли вы написать похожую процедуру Блупа, которая проверяла бы наличие у числа свойства Черепахи (или Ахилла)? Попытайтесь! Если вам это не удается, то только лишь потому, что вы не знаете, какой будет верхняя граница? Возможно ли, что существует какое-то фундаментальное препятствие, вообще не позволяющее формулировать подобные алгоритмы в Блупе? А что, если задать те же вопросы касательно свойства интересности, определенного в Диалоге?

Ниже я привожу некоторые функции и свойства; попробуйте определить для каждого из них, является ли оно примитивно-рекурсивным (то есть, программируемым на Блупе). Для этого вы должны будете хорошенько подумать, какой тип операций потребуется для соответствующих вычислений и можно ли определить потолок для всех циклов данной процедуры.

ФАКТОРИАЛ [N] = N! (ФАКТОРИАЛ ОТ N).

(Например, ФАКТОРИАЛ [4] = 24).

ОСТАТОК [M.N] = остаток после деления М на N.

(Например, ОСТАТОК [24,7] = 3).

ЦИФРА π [N] = N-ная цифра π после запятой.

(Например, ЦИФРА π [1] = 1,

ЦИФРА π [2] = 4,

ЦИФРА π [1 000 000] = 1).

ФИБО[М] = N-ное число ряда Фибоначчи.

(Например, ФИБО [9] = 34).

ПРОСТОЕ ЧИСЛО ЗА [N] = наименьшее простое число, следующее за N.

(Например, ПРОСТОЕ ЧИСЛО ЗА [33] = 37).

СОВЕРШЕННОЕ [N] = N-ное «совершенное» число, такое как, например, 28, чьи множители в сумме дают само это число: 28 =1+2+4+7+14.

(Например, СОВЕРШЕННОЕ [2] = 28).

ПРОСТОЕ? [N] = ДА если N простое число, в противном случае, НЕТ.

СОВЕРШЕННОЕ [N]? = ДА если N совершенное число, в противном случае, НЕТ.

ОБЫКНОВЕННОЕ? [А, В, С, N] = ДА, если A ^N+ В ^N= С ^N верно; в противном случае, НЕТ.

(Например, ОБЫКНОВЕННОЕ ? [3, 4, 5, 2] = ДА,

ОБЫКНОВЕННОЕ ? [3, 4, 5, 3] = НЕТ).

ПЬЕР? [А,В,С] = ДА, если A ^N+ В ^N= С ^N верно для N > 1; в противном случае, НЕТ.

(Например, ПЬЕР? [3, 4, 5] = ДА,

ПЬЕР? [1,2,3] = НЕТ).

ФЕРМА? [N] == ДА, если А ^N + В ^N = С ^N верно для неких положительных величин А, В, и С; в противном случае, НЕТ.

(Например, ФЕРМА? [2] = ДА).

ЧЕРЕПАШЬЯ ПАРА? [M, N] = ДА если M и M + N простые числа; в противном случае, НЕТ.

(Например, ЧЕРЕПАШЬЯ ПАРА? [5, 1742] = ДА.

ЧЕРЕПАШЬЯ ПАРА? [5, 100] = НЕТ).

ЧЕРЕПАХА [N] = ДА, если N - разность двух простых чисел, в противном случае, НЕТ.

(Например, ЧЕРЕПАХА [1742] = ДА,

ЧЕРЕПАХА [7] = НЕТ).

ХОРОШО СФОРМИРОВАННАЯ MIU? [N] = ДА, если N, в качестве строчки MIU, хорошо сформировано; в противном случае, НЕТ.

(Например, ХОРОШО СФОРМИРОВАННАЯ MIU? [310] = ДА,

ХОРОШО СФОРМИРОВАННАЯ MIU? [415] = НЕТ).

ПАРА ДОКАЗАТЕЛЬСТВА MIU? [М, N] = ДА. если М, рассматриваемое как  последовательность  строчек MIU, является деривацией N, рассматриваемого  как строчка системы MIU; в противном случае, НЕТ.

(Например, ПАРА ДОКАЗАТЕЛЬСТВА MIU? [3131131111301, 301] = ДА,

ПАРА ДОКАЗАТЕЛЬСТВА MIU? [311130, 30] = НЕТ).

ТЕОРЕМА MIU? [N]= ДА, если N, в качестве строчки MIU, является теоремой; в противном случае, НЕТ.

(Например, ТЕОРЕМА MIU? [311] = ДА,

ТЕОРЕМА MIU? [30]= НЕТ,

ТЕОРЕМА MIU? [701]= НЕТ).

ТЕОРЕМА ТТЧ? [N]= ДА, если N, в качестве строчки ТТЧ, является теоремой; в противном случае, НЕТ.

(Например, ТЕОРЕМА ТТЧ? [666111666] = ДА,

ТЕОРЕМА ТТЧ?[123666111666] = НЕТ,

ТЕОРЕМА ТТЧ? [7014] = НЕТ).

ЛОЖНО? [N)= ДА, если N, в качестве строчки ТТЧ, представляет собой ложное утверждение теории чисел; в противном случае, НЕТ.

(Например,  ЛОЖНО? [666111666]= НЕТ,

ЛОЖНО? [223666111666]= ДА,

ЛОЖНО? [7014]= НЕТ).

Последние семь примеров особенно важны для наших будущих метаматематических исследований, поэтому они заслуживают самого пристального внимания.

Выразимость и представимость.

Прежде, чем рассмотреть еще несколько интересных вопросов, касающихся Блупа, и перейти к его родственнику, Флупу, давайте вернемся к тому, зачем нам вообще понадобился Блуп, и к его связи с ТТЧ. Ранее я сказал, что критическая масса, необходимая формальной системе для приложения метода Гёделя, достигается тогда, когда в этой системе представимы все примитивно-рекурсивные понятия. Что это означает? Прежде всего, мы должны различать между понятиями представимости и выразимости. Выразить предикат означает просто перевести его с русского языка на язык формальной системы. Это не имеет ничего общего с теоремностью. С другой стороны, если предикат представлен, это означает, что.

(1) Все истинные примеры этого предиката — теоремы;

(2) Все ложные примеры этого предиката — не теоремы.

Под «примером» я имею в виду строчку, которая получается при замене всех свободных переменных на числовые величины. Например, предикат m + n = k представлен в системе рг, поскольку каждый истинный пример этого предиката — теорема, и каждый ложный — не теорема. Таким образом, каждый частный случай сложения, истинный или ложный, переводится в разрешимую строчку системы рг. Однако система pr не способна выразить — и меньше того, представить — никакие другие свойства натуральных чисел. Она была бы слабеньким кандидатом в соревновании систем, способных символизировать теорию чисел.

ТТЧ, со своей стороны, способна выразить практически любой теоретико-численный предикат; например, легко написать строчку ТТЧ, выражающую предикат «b имеет свойство Черепахи». Таким образом, в смысле выразительной мощи ТТЧ — это именно то, что нам требуется.

Однако вопрос «Какие свойства представлены в ТТЧ?» эквивалентен вопросу «Насколько мощной аксиоматической системой является ТТЧ?» Можно ли сказать, что в ней представлены все возможные предикаты? Если это так, то ТТЧ может ответить на любой вопрос теории чисел — то есть она полна.

Примитивно-рекурсивные предикаты представлены в ТТЧ.

Хотя вскоре выяснится, что ее полнота не более чем химера, ТТЧ полна, по крайней мере, в отношении примитивно-рекурсивных предикатов. Иными словами, любое высказывание теории чисел, чья истинность или ложность могут быть разрешены компьютером за некое предсказуемое время, разрешимо также в ТТЧ. Иными словами,

Если на Блупе можно написать тест для некого свойства натуральных чисел, то это свойство представлено в ТТЧ.

Есть ли функции, не являющиеся примитивно-рекурсивными?

Свойства чисел, которые можно обнаружить с помощью тестов Блупа, широко варьируются: это простота чисел, их совершенность, наличие у них свойства Гольдбаха, то, является ли число степенью двух и т. д. Логично было бы спросить, всякое ли свойство чисел может быть обнаружено соответствующей программой Блупа. Нас не должно смущать, что мы пока не можем проверить число на его интересность. Это может означать лишь то, что у нас не хватает знаний; возможно, если как следует поискать, нам удалось бы найти верхнюю границу соответствующего цикла. Тогда мы могли бы тут же написать тест Блупа. То же самое можно сказать и о свойстве Черепахи.

Следовательно, вопрос в том, можно ли найти потолок для любого цикла — или же теории натуральных чисел присуща некая беспорядочность, мешающая нам предсказать заранее длину некоторых вычислений? Удивительно то, что верно второе, и сейчас мы увидим, почему. Наверное, именно такой тип рассуждений свел с ума Пифагора, впервые доказавшего иррациональность корня из двух. В нашем доказательстве мы будем использовать знаменитый диагональный метод, изобретенный основателем теории множеств Георгом Кантором.

Клуб Б, номера-индексы и Белые Программы.

Для начала представим себе забавное понятие: некий клуб, членами которого являются все возможные программы Блупа. Нет нужды говорить, что число членов этого клуба (назовем его клубом Б) бесконечно. Рассмотрим часть этого клуба, так сказать, подклуб, полученный после трех последовательных фильтрующих операций. Первый фильтр оставит нам только программы без вызова. Из этого подклуба мы уберем все тесты, оставив только функции. (Кстати, последняя процедура программ без вызова определяет, является ли программа тестом или функцией.) Третий фильтр удержит только функции с единственным входным параметром. Что у нас остается?

Полный набор всех безвызовных программ Блупа, вычисляющих функции с единственным входным параметром.

Назовем такие специальные функции Белыми Программами.

Следующим шагом будет установление для каждой Белой Программы определенного номера-индекса. Как это можно сделать? Легче всего составить список Белых Программ согласно их длине: самая короткая возможная программа будет #1, вторая по длине — #2 и т. д. Разумеется, некоторые программы окажутся одинаковой длины — в этом случае мы будем пользоваться также алфавитным порядком. Термин «алфавитный порядок» здесь употребляется в широком смысле: алфавит включает как кириллические, так и латинские буквы, а также все специальные символы Блупа в неком произвольно установленном порядке, как, например, следующий:

А Б В Г Д Е Ж З И Й К Л М Н О П.

Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Э Ь Ю Я.

A B C D E F G H I J K L M N.

O P Q R S T U V W X Y Z + Х.

1 0 2 3 4 5 6 7 8 9 <= = <  >

( ) [ ] { } - ' ? : ; , .

В конце находится скромный интервал, пустое место! Всего 88 символов. Для удобства, мы можем поместить все Белые Программы длины 1 в том 1, программы их двух символов — в том 2 и т. д. Ясно, что первые несколько томов будут совершенно пустыми, в то время как все последующие тома будут заполнены (каждый том будет содержать конечное количество записей). Самой короткой Белой Программой будет следующая:

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «А» [В]:

БЛОК 0:НАЧАЛО.

БЛОК 0: КОНЕЦ.

Эта глупенькая мясорубка выдает 0, что бы в нее ни засунули. Эта программа находится в томе 59, поскольку в ней 59 символов (считаются все необходимые интервалы, включая те, что разделяют строчки).

Тома, следующие за томом 59, вскоре станут претолстыми, поскольку существуют миллионы различных способов комбинировать символы и составлять Белые Программы. Однако мы не будем печатать здесь весь этот бесконечный каталог; нам важно знать только то, что он четко определен и что каждая Белая Программа Блупа имеет свой собственный, неповторяющийся индекс. Именно в этом — основная идея.

Давайте определим функцию, вызываемую k-нон Белой Программой следующим образом:

Belprogram {#k}[N].

Здесь k — индекс программы, и N — единственный параметр входа. Например, Белая Программа #12 может выдать результат, вдвое больший ее входа:

Belprogram {#12}[N] = 2 * N.

Смысл вышеприведенного уравнения в том, что программа, приведенная слева, выдает такую же величину, которую получил бы человек, пользуясь обыкновенным алгебраическим выражением справа. Еще один пример: Белая Программа # 5000 может сосчитать куб числа на основании входного параметра:

Belprogram {#5000}[N] = N³

Диагональный метод.

Давайте теперь применим обещанный трюк — Канторов диагональный метод. Возьмем каталог всех Белых Программ и используем его для определения новой функции с одной переменной — Beldiag [N]. Этой функции не окажется нигде в нашем списке (поэтому ее название выделено курсивом). Тем не менее, Beldiag будет хорошо определенной, Вычислимой функцией с одной переменной; таким образом, нам придется заключить, что некоторые функции просто невозможно запрограммировать на Блупе. Вот определение Beldiag [N]:

Уравнение (1) … Beldiag [N]: = 1 + Belprogram {#N}[N].

Стратегия здесь следующая: в каждую «мясорубку» закладывается ее собственный индекс, и к результату прибавляется 1. Для примера, давайте найдем Beldiag [12]. Мы знаем, что Belprogram [N] — это функция 2N; следовательно, Beldiag [12] должна иметь значение 1 + 2 * 12, то есть 25. Так же, Beldiag [5000] имела бы значение 125 000 000 001, поскольку она на единицу больше куба 5000. Подобным образом можно найти Beldiag любого аргумента.

Интересно то, что сама Beldiag [N] не представлена в каталоге Белых Программ. Она просто не может там быть — и вот почему: чтобы быть одной из Белых Программ, каждая программа должна иметь индекс. Возьмем, к примеру, Белую Программу #X. Этот факт выражается следующим уравнением:

Уравнение (2) … Beldiag [N]: = Belprogram {#X}[N].

Однако между уравнениями (1) и (2) есть противоречие, которое становится явным, когда мы пытаемся вычислить величину Beldiag [X]. Для этого мы должны заменить N на X в обоих уравнениях. В случае уравнения (1) мы получим:

Beldiag [X] = 1 + Belprogram {#X}[X].

С другой стороны, произведя замену в уравнении (2), мы получаем:

Beldiag [X] = Belprogram {#X}[X].

Но Beldiag [N] не может быть равен одновременно и числу, и его последователю, как утверждают эти два уравнения. Нам придется вернутся назад и избавиться от допущения, на котором основано это противоречие. Единственным кандидатом оказывается уравнение (2), утверждающее, что Beldiag [N] может быть закодировано как Белая Программа Блупа. И это доказывает, что Beldiag не является примитивно-рекурсивной функцией. Таким образом, нам удалось достигнуть своей цели и разрушить милое, но наивное убеждение Ахилла о том, что любая теоретико-числовая функция может быть вычислена за предсказуемое количество шагов.

С Beldiag [N] происходят довольно интересные вещи. Например, вы можете пораздумывать над следующим фактом: для каждого конкретного N можно предсказать число необходимых шагов, но при этом невозможно найти общий рецепт для предсказания длины вычислений Beldiag [N]. Перед нами — бесконечный заговор, родственный идее Черепахи о «бесконечных совпадениях», а также ω-неполноте. Здесь, однако, мы не будем подробно останавливаться на этих отношениях.

Первоначальный диагональный аргумент Кантора.

Почему этот прием называется диагональным аргументом? Этот термин восходит к первоначальному диагональному аргументу Кантора, на котором впоследствии были основаны многие другие доводы (в том числе наш). Объяснение первоначального аргумента Кантора немного отвлечет нас от нашей темы, но все же это стоит сделать. Кантор тоже хотел показать, что некий предмет не состоит в определенном списке. Конкретнее, он хотел доказать, что если бы был создан список действительных чисел, то некоторые действительные числа неизбежно очутились бы вне этого списка; таким образом, понятие полного списка действительных чисел уже само по себе противоречиво.

Необходимо иметь в виду, что это верно не только для конечных, но и для бесконечных списков. Это гораздо более важный результат, чем утверждение типа: «Количество действительных чисел бесконечно, следовательно, оно не может содержаться ни в каком конечном списке.» Основная мысль Канторова результата заключается в том, что существуют два типа бесконечности: одна из них описывает, сколько отдельных записей может быть в бесконечном списке, в то время как другая — сколько существует действительных чисел (или сколько есть точек на линии или ее отрезке). Вторая бесконечность «больше», в том смысле, что действительные числа невозможно уместить в таблице, длина которой описана с помощью первой бесконечности. Посмотрим теперь, как аргумент Кантора использует диагональ в буквальном смысле.

Возьмем действительные числа между 0 и 1. Предположим, что возможно составить такой бесконечный список, в котором каждое положительное число N сопоставлено с действительным числом r(N) между 0 и 1, и где встречается каждое число между нулем и единицей. Поскольку действительные числа представлены бесконечными дробями, мы можем предположить, что начало списка выглядит так:

R(1): ,1  4  1  5  9  2  6  5  3  .  .  .  .  .  .  .

R(2): ,3  3  3  3  3  3  3  3  3  .  .  .  .  .  .  .

R(3): ,7  1  8  2  8  1  8  2  8  .  .  .  .  .  .  .

R(4): ,4  1  4  2  1  3  5  6  2  .  .  .  .  .  .  .

R(5): ,5  0  0  0  0  0  0  0  0  .  .  .  .  .  .  .

Цифры, идущие вниз по диагонали, выделены жирным шрифтом. Они будут использованы для получения того действительного числа d, которое находится между 0 и 1, но которое, как мы увидим, не состоит в списке. Чтобы получить d, вы берете диагональные цифры по порядку и меняете каждую из них на какую-либо иную цифру. После этого вы добавляете слева запятую, указывающую на десятичную дробь, и ваше число d готово! Разумеется, есть множество способов поменять одну цифру на другую и, соответственно, множество различных d. Предположим, например, что мы решили отнять от каждой диагональной цифры 1 (будем считать, что 0-1=9). Тогда нашим числом d будет:

,0 2 7 1 9 …

Мы построили его таким образом, что.

Первая цифра d отличается от первой цифры r (1);

Вторая цифра d отличается от второй цифры  r (2);

Третья цифра d отличается от третьей цифры r (3);

… И так далее.

Следовательно,

d отличается от r (1);

d отличается от r (2);

d отличается от r (3);

… И так далее.

Иными словами, d не находится в списке!

Что доказывает диагональный метод?

Основное различие между методом Кантора и нашим методом заключается в том, какое предположение мы решили изменить. В Канторовском методе этим предположением была сомнительная идея, что подобный список вообще возможен. Построение d доказало, что полную таблицу действительных чисел составить невозможно; иными словами, множество целых чисел не достаточно велико, чтобы пронумеровать множество всех действительных чисел. С другой стороны, в нашем доказательстве мы знаем, что список Белых Программ можно составить: множество целых чисел достаточно велико, чтобы пронумеровать множество всех Белых Программ. Поэтому нам приходится искать другую сомнительную идею. Ею оказывается предположение, что Beldiag [N] может быть закодировано как Белая Программа Блупа. Именно в этом — тонкое различие в приложении диагонального метода.

Это может стать понятнее, если мы применим тот же метод к «Списку Всех Великих Математиков» в Диалоге. Диагональ этого списка читается «Dboups». Заменив каждую букву на предыдущую букву латинского алфавита, мы получим «Cantor». Из этого возможны два заключения. Если вы твердо убеждены в том, что список полон, то вам приходится заключить, что Кантор — не Великий Математик, поскольку его имени нет в списке. С другой стороны, если вы убеждены в том, что Кантор — Великий Математик, то должны заключить, что Список Всех Великих Математиков неполон, поскольку этого имени там нет! (Горе тем несчастным, кто твердо убежден и в том, и в другом!) Первый случай соответствует нашему доказательству того, что Beldiag [N] — не примитивно-рекурсивная функция; второй — канторовскому доказательству того, что список действительных чисел неполон.

Канторовское доказательство использует диагональ в буквальном смысле слова. Другие «диагональные» доказательства основаны на более общем понятии, абстрагированном от геометрического смысла слова. В сердце диагонального метода лежит использование одного и того же целого числа двумя разными способами — можно сказать, что одно и то же число используется на двух разных уровнях — благодаря чему удается построить некий объект, не состоящий в определенном списке. Первый раз это число служит как вертикальный индекс, второй раз — как горизонтальный индекс. В Канторовском построении это хорошо видно. Что касается функции Beldiag [N], то там мы используем одно и то же число на двух различных уровнях: сначала как индекс Белой Программы и потом как входной параметр.

Рис. 73. Георг Кантор.

Коварная повторяемость диагонального метода.

С первого взгляда, аргумент Кантора может показаться не очень-то убедительным. Нельзя ли его как-нибудь обойти? Может быть, если добавить к списку наше число d, то список окажется полным? Однако если подумать, то становится ясно, что это ничем не поможет, поскольку, как только это число займет свое место в списке, к последнему снова можно будет применить диагональный метод, результатом чего будет недостающее в новом списке число d'. Сколько бы раз вы не конструировали новые числа d и не добавляли их к списку в надежде его дополнить, вы все еще находитесь на крючке Канторовского метода. Вы даже можете попытаться построить такую таблицу действительных чисел, которая перехитрила бы диагональный метод, каким-то образом учитывая все его трюки вместе с самой повторяемостью. Это довольно интересное упражнение; однако, занявшись этим, вы очень скоро поймете, что, как бы вы не исхитрялись, вам не удастся сорваться с крючка Канторовского метода. Можно сказать, что любая так называемая «таблица всех действительных чисел» обязательно запутается в своих же сетях.

Повторяемость диагонального метода Кантора похожа на повторяемость дьявольского метода Черепахи, которым она разбивала Крабьи патефоны по мере того, как они становились все качественнее и — по мнению Краба — все «совершеннее». Ее метод заключался в создании для каждого патефона специальной записи, которую тот был не в состоянии воспроизвести. Эта любопытная повторяемость не случайно является общей чертой обоих методов; в действительности, «Акростиконтрапунктус» вполне мог бы называться «Акростиканторпунктусом». Более того, как Черепаха намекала наивному Ахиллу, события в «Акростиконтрапунктусе» — перифраз построения, которое Гёдель использовал для доказательства своей Теоремы Неполноты; из этого следует, что Гёделево построение сродни диагональному методу. Это станет очевидным в следующих двух главах.

От Блупа к Флупу.

Мы определили примитивно-рекурсивные функции и примитивно-рекурсивные свойства натуральных чисел с помощью программ, написанных на языке Блуп. Мы также показали, что Блуп не описывает всех функций натуральных чисел, которые можно выразить словами. Мы даже построили, пользуясь Канторовским методом, «не-Блупабельную» функцию Beldiag [N]. Что же именно в Блупе делает невозможным представить в нем функцию Beldiag [N]? Можно ли улучшить Блуп таким образом, что Beldiag [N] станет в нем представимой?

Определяющей чертой Блупа была ограниченность его циклов. Что, если мы опустим это требование и создадим второй язык, под названием Флуп? Флуп будет идентичен Блупу во всем, кроме одного: в нем можно будет иметь циклы как с потолком, так и без потолка (на самом деле, потолок здесь будет включаться в циклы исключительно для элегантности). Эти новые циклы будут называться MU-циклы, следуя обозначению, принятому в математической логике, где «свободный (неограниченный) поиск» обычно обозначается символом «μ — оператор». Таким образом, цикл в Флупе может выглядеть так:

MU-ЦИКЛ:

БЛОК n: НАЧАЛО.

.

.

.

БЛОК n: КОНЕЦ.

Эта характеристика позволит нам написать на Флупе тесты для свойства Черепахи и свойства интересности — тесты, которые мы не могли создать на Блупе из-за того, что поиск там мог оказаться потенциально бесконечным. Интересующиеся читатели могут попробовать написать на Флупе следующий тест на интересности:

(1) Если вводной параметр N оказывается интересным числом, программа останавливается и выдает ответ ДА.

(2) Если N — неинтересное число, порождающее любой закрытый цикл, отличный от 1-4-2-1-4-2-1-…, программа останавливается и выдает ответ НЕТ.

(3) Если N — неинтересное число, порождающее «бесконечно возрастающую прогрессию», программа никогда не останавливается. Это «не-отвечание» и есть ответ Флупа. He-ответ Флупа странным образом напоминает не-ответ Джошу — «МУ».

Ирония (3) заключается в том, что ВЫХОД всегда принимает значение НЕТ, но при этом он недоступен, поскольку программа все еще работает. Неприятная третья альтернатива — это та цена, которую нам приходится платить за право писать свободные циклы. Незаконченность всегда будет теоретической альтернативой для всех программ Флупа, включающих вариант MU-цикла. Разумеется, множество программ Флупа будут заканчиваться для всех возможных величин вводного параметра. Например, как я уже говорил, большинство людей, изучавших свойство интересности, считают, что программы Флупа, подобные описанной выше, всегда будут заканчиваться — и, более того, всегда ответом ДА.

Оканчивающиеся и неоканчивающиеся программы Флупа.

Было бы очень хорошо, если бы нам удалось разделить все процедуры Флупа на два класса: оканчивающиеся (терминаторы) и неоканчивающиеся (не-терминаторы). Первые всегда будут рано или поздно останавливаться, независимо от входных параметров и от наличия в нем MU-циклов. Вторые будут работать до бесконечности по крайней мере при одном из возможных выборов входного параметра. Если бы всегда можно было, внимательно рассмотрев данную программу Флупа, определить к какому типу она принадлежит, это привело бы к важным последствиям (как мы скоро увидим). Нет нужды говорить, что сама операция определения классов должна была 6ы принадлежать к оканчивающемуся типу, иначе бы от нее было мало пользы.

Трюки Тьюринга.

Может быть, нам удастся заставить какую-нибудь из процедур самого Флупа заняться этой проверкой? Загвоздка здесь в том, что процедуры Флупа принимают в качестве вводных параметров только числа, а не программы. Однако это препятствие можно обойти … закодировав программы с помощью чисел! Этот ловкий трюк — не что иное, как Гёделева нумерация в одной из многих своих манифестаций. Каждый из 88 символов алфавита Флупа получит свой «кодон»: 901, 902, …988. Таким образом, каждая программа Флупа приобретает некий длинный Гёделев номер. Например, самая короткая функция Блупа (которая в то же время является оканчивающейся программой Флупа).

ОПРЕДЕЛИТЬ ПРОЦЕДУРУ «А» [В]:

БЛОК 0:НАЧАЛО.

БЛОК 0: КОНЕЦ.

Получит Гёделев номер, частично показанный ниже:

915,916,917,906,905,906,912,909,919,929,....... 911, 915,914,906,923,987.

О   П   Р   Е   Д   Е   Л   И   Т   Ь           К    О   Н   Е   Ц   .

Теперь нам нужен тест Блупа под названием ТЕРМИНАТОР?, который отвечал бы ДА, если входной параметр являлся бы кодом оканчивающейся программы Флупа, и НЕТ — в противном случае. Таким образом, если нам повезет, мы сможем заставить машину отличать терминаторы от не-терминаторов. Однако хитроумный аргумент, придуманный Аланом Тьюрингом, доказал, что никакая программа Блупа не сможет безошибочно находить это различие. Его идея весьма напоминает Гёделев метод и, таким образом, находится в близком родстве с диагональным методом Кантора. Не буду приводить ее здесь; достаточно сказать, что идея Тьюринга заключалась в том, чтобы ввести в программу ее собственный Гёделев номер. Это, однако, весьма непросто, все равно что ухитриться процитировать какое-то предложение внутри него самого. Для этого пришлось бы процитировать также и саму цитату… и так далее, и тому подобное. Очевидно, что это приводит к бесконечному регрессу. Однако Тьюринг придумал ловкий трюк, позволяющий скормить программе ее собственный Гёделев номер. В следующей главе я приведу решение этой проблемы в ином контексте. Однако сейчас мы пойдем к той же цели другой дорогой — а именно, постараемся доказать, что такой тест невозможен. Читатели, которые хотят ознакомиться с элегантной и простой версией метода Тьюринга, могут обратиться к статье Хоара и Аллисона (Hoar and Allison), упоминающейся в библиографии.

Программа-тест терминаторов была бы волшебной.

Прежде, чем окончательно распроститься с этим понятием, давайте посмотрим, почему иметь такую программу было бы так замечательно. Такой тест был бы чем-то вроде волшебной палочки, которая могла бы одним взмахом разрешить все проблемы теории чисел. Предположим, мы захотели бы узнать, является ли Вариация Гольдбаха истинным предположением — иными словами, все ли числа обладают свойством Черепахи. Для начала мы написали бы тест на Флупе под названием ЧЕРЕПАХА?, который проверял бы, есть ли у вводного параметра данное свойство. Дефект этой программы — то, что она не кончается, если ввод не обладает свойством Черепахи — здесь превращается в достоинство, поскольку теперь мы можем проверить процедуру ЧЕРЕПАХА? на ее кончаемость. Если наш тест отвечает ДА, это значит, что ЧЕРЕПАХА? кончается для всех вводных параметров — иными словами, все числа обладают свойством Черепахи. Ответ НЕТ означал бы, что имеется некое число, обладающее свойством Ахилла. Ирония заключается в том, что мы никогда не используем саму программу ЧЕРЕПАХА? — мы только ее проверяем.

Идея решения любой проблемы теории чисел путем кодирования ее в программу и затем проверки этой программы на кончаемость сродни идее о проверке подлинности буддистского коана путем кодирования его в сложенную цепочку и затем проверяя на наличие буддистской природы уже эту цепочку. Может быть, Ахилл был прав, предполагая, что нужная информация может лежать ближе к поверхности в одном отображении, чем в другом.

Клуб Ф, числа-индексы и Зеленые Программы.

Довольно мечтать — пора заняться делом! Как можно доказать, что тест на кончаемость в принципе невозможен? Для этого мы попытаемся применить диагональный аргумент к Флупу, так же, как мы это делали с Блупом. Мы увидим, что между этими двумя случаями есть небольшая, но решающая разница.

Так же, как в случае Блупа, вообразим клуб, членами которого являются все программы Флупа. Мы будем называть его «Клубом Ф». Теперь проведем с ним те же три фильтрующих операции, после чего мы получим:

Полный клуб всех безвызовных программ Флупа, которые вычисляют функции с одним вводным параметром.

Давайте назовем эти специальные программы Флупа Зелеными Программами (поскольку они могут идти, никогда не останавливаясь, словно машины на зеленый свет).

Теперь, точно так же как мы это сделали с Белыми Программами, дадим каждой Зеленой Программе индекс и организуем их в каталог, каждый том которого состоит из программ определенной длины, расположенных в алфавитном порядке.

До сих пор мы просто повторяли с Флупом то, что ранее проделали с Блупом. Посмотрим теперь, удастся ли нам скопировать последнюю часть — диагональный метод. Попробуем определить диагональную функцию:

Zeldiag [N] = 1 + Zelprogram {#N}[N].

Тут получается заминка: функция Zeldiag [N] может не иметь определенного значения выхода для всех значений входного параметра N. Это происходит потому, что при «фильтровании» мы не очистили Клуб Ф от всех неоканчивающихся программ — таким образом, у нас нет гарантии, что мы сможем вычислить Zeldiag [N] для всех значений N. Иногда мы можем ввести вычисления, которые никогда не окончатся. Диагональный аргумент в этом случае не годится, так как для его успешного приложения диагональная функция должна иметь значение для всех возможных входных параметров.

Проверка на кончаемость и Красные Программы.

Чтобы поправить положение, мы могли бы использовать тест на кончаемость — если бы таковой существовал. Давайте предположим на минуту, что такой тест имеется, и используем его в качестве нашего четвертого фильтра. Идя по списку Зеленых Программ, мы начинаем отбрасывать одну за другой все не-терминаторы, так что в конце у нас остается:

Полный клуб всех безвызовных программ Флупа, которые вычисляют функции с одним входным параметром и которые оканчиваются для всех его значений.

Давайте назовем эти специальные программы Флупа Красными Программами (поскольку они всегда должны останавливаться, как машины на красный свет). Теперь мы можем применить диагональный аргумент. Определим:

Krasdiag [N] = 1 + Krasprogram {#N}[N].

Точно так же, как в случае с функцией Белдиаг, мы должны заключить, что Krasdiag [N] — хорошо определенная, вычисляемая функция одной переменной, которая не находится в списке Красных Программ и, следовательно, ее невозможно вычислить даже с помощью мощного языка Флуп. Не пора ли нам перейти к Глупу?

Глуп — …

Что же такое Глуп? если Флуп — это освобожденный от цепей Блуп, то Глуп должен, в свою очередь, быть освобожденным от цепей Флупом. Но как же можно снять цепи дважды? Как можно создать язык, более мощный, чем Флуп? Krasdiag [N] оказалась функцией, значение которой умеем вычислять только мы, люди, поскольку мы подробно описали всю процедуру на русском языке — однако эту функцию, по-видимому, невозможно запрограммировать на языке Флуп. Это — весьма серьезная проблема, поскольку никто пока не нашел компьютерного языка, более мощного, чем Флуп.

Мощность компьютерных языков в последнее время была объектом тщательных исследований. Нам самим не придется этим заниматься; упомянем только, что существует целый класс компьютерных программ с точно такой же выразительной мощностью, как Флуп, в том смысле, что любое вычисление, программируемое на одном языке, может быть запрограммировано на всех остальных языках. Интересно то, что почти любая попытка создать достойный внимания компьютерный язык приводит к созданию языка этого класса, то есть языка с выразительной мощностью Флупа. Приходится попотеть, чтобы создать достаточно интересный компьютерный язык слабее этих языков. Блуп, разумеется, пример более слабого языка, но это — скорее исключение, чем правило. Дело в том, что существует некий естественный путь создания алгоритмических языков, так что разные люди, работая независимо друг от друга, обычно создают эквивалентные языки, отличающиеся скорее стилем, чем степенью мощности.

… Ни что иное как миф.

В действительности, большинство специалистов считают, что для описания вычислений не может существовать более мощных языков, чем языки, эквивалентные Флупу. Эта гипотеза была сформулирована в 1930-х годах двумя людьми, работавшими независимо друг от друга. Об одном из них, Алане Тьюринге, мы еще будем говорить; другим был один из ведущих логиков этого столетия, Алонзо Чёрч. Гипотеза получила название Тезис Чёрча-Тьюринга. Принимаем Тезис Ч-Т за истину, мы должны заключить, что Глуп — не более, чем миф, поскольку во Флупе нет никаких ограничений, которые можно было бы снять; его мощность невозможно усилить, «сняв с него цепи», как мы это сделали с Блупом.

Это ставит нас в неудобное положение: нам приходится заключить, что люди могут вычислить Krasdiag [N] для любого N, в то время как компьютер этого сделать не может. Дело в том что если бы это было в принципе возможно, это было бы возможно на Флупе — однако мы только что выяснили, что на Флупе этого нельзя сделать по определению. Это такое странное заключение, что нам придется как следует рассмотреть, на чем оно основано. Одним из краеугольных камней нашего построения было, если вы помните, сомнительное предположение о существовании разрешающей процедуры, способной отличить заканчивающиеся программы Флупа от незаканчивающихся. Возможность такой процедуры показалась подозрительной уже тогда, когда мы увидели, что она помогла бы разрешить все проблемы теории чисел одинаковым путем. Теперь у нас есть две причины, чтобы считать тест на кончаемость мифом; видимо, невозможно, пропустив программы Флупа через центрифугу, отличить терминаторы от не-терминаторов.

Скептики могут возразить: а где же строгое доказательство невозможности подобного теста? Это возражение имеет смысл. Однако в подходе Тюринга мы находим более строгое обоснование того, что на языке класса Флупа невозможно написать программу, проверяющую программы Флупа на кончаемость.

Тезис Чёрча-Тьюринга.

Посмотрим, что представляет из себя этот Тезис. Мы будем говорить о нем во всех подробностях в главе XVII; до тех пор мы воздержимся от его обсуждения, а здесь дадим лишь пару версий Тезиса. Далее следуют три родственных способа его выражения:

(1) То, что могут вычислить люди, могут вычислить и машины.

(2) То, что могут вычислить машины, может быть вычислено с помощью Флупа.

(3) То, что могут вычислить люди, может быть вычислено с помощью Флупа.

Терминология: общерекурсивный и частично рекурсивный.

В этой главе мы дали довольно широкий обзор некоторых понятий теории чисел и их соотношения с вычисляемыми функциями. Это очень плодотворное поле для исследований, поле, где переплетается теория вычислительной техники и современная математика. Прежде, чем заключить эту главу, я хочу ввести стандартные термины для понятий, с которыми мы здесь познакомились.

Как я уже говорил, выражение «вычислимый на Блупе» эквивалентно выражению «примитивно-рекурсивный». С другой стороны, функции, вычислимые на Флупе, можно подразделить на две категории. Функции, вычислимые с помощью кончающихся программ Флупа, называются общерекурсивными; функции, вычислимые только с помощью не кончающихся программ Флупа, называются частично рекурсивными. (То же самое применимо и к предикатам.) Многие, говоря о «рекурсивных» функциях, на самом деле имеют в виду их «общерекурсивную» разновидность.

Мощь ТТЧ.

Интересно, что ТТЧ настолько мощна, что в ней представлены не только все примитивно-рекурсивные предикаты, но и все общерекурсивные предикаты. Мы не будем приводить здесь доказательство обоих фактов, поскольку это увело бы нас в сторону от нашей цели — показать, что ТТЧ неполна. Если бы ТТЧ не могла выразить какие-либо примитивно-рекурсивные или общерекурсивные предикаты, ее неполнота была бы неинтересна — так почему бы нам не согласиться с тем, что все эти предикаты в ней выразимы, и не доказать, что она неполна в другом, более интересном смысле?