ГЕДЕЛЬ, ЭШЕР, БАХ: эта бесконечная гирлянда.

Водоворот Эшера, где скрещиваются все уровни.

Рис. 142. М. К. Эшер. Картинная галерея (литография, 1956).

Поразительно красивая и в то же время странно тревожащая иллюстрация «глаза» циклона, порожденного Запутанной Иерархией, дана нам Эшером в его «Картинной галерее» (рис. 142). На этой литографии изображена картинная галерея где стоит молодой человек, глядя на картину корабля в гавани небольшого городка, может быть, мальтийского, судя по архитектуре, с его башенками, куполами и плоскими каменными крышами, на одной из которых сидит на солнце мальчишка, а двумя этажами ниже какая-то женщина — может быть, мать этого мальчишки — глядит из окна квартиры, расположенной прямо над картинной галереей, где стоит молодой человек, глядя на картину корабля в гавани небольшого городка, может быть, мальтийского — Но что это!? Мы вернулись к тому же уровню, с которого начинали, хотя логически этого никак не могло случиться. Давайте нарисуем диаграмму того, что мы видим на этой картине (рис 143).

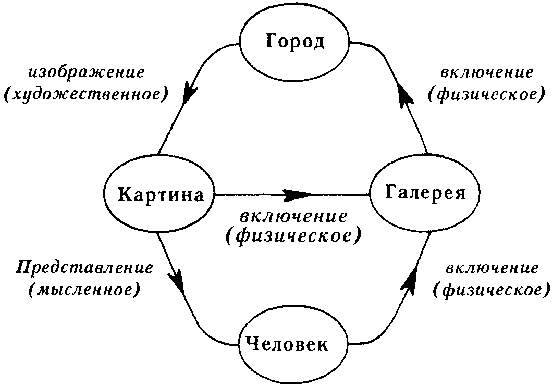
Рис. 143. Абстрактная диаграмма «Картинной галереи» М. К. Эшера.

На этой диаграмме показаны три вида включения. Галерея физически включена в город («включение»); город художественно включен в картину («изображение»); картина мысленно включена в человека («представление»). Хотя эта диаграмма может показаться точной, на самом деле она произвольна, поскольку произвольно количество показанных на ней уровней. Ниже представлен другой вариант верхней половины диаграммы (рис. 144):

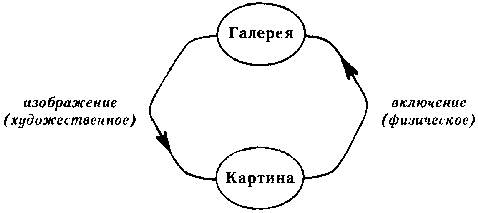
Рис. 144. Сокращенная версия предыдущей диаграммы.

Мы убрали уровень «города»; хотя концептуально он полезен, без него можно вполне обойтись. Рис. 144 выглядит так же, как диаграмма «Рисующих рук»: это двухступенчатая Странная Петля. Разделительные знаки произвольны, хотя и кажутся нам естественными. Это видно яснее из еще более сокращенной диаграммы «Картинной галереи»:

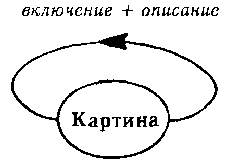
Рис. 145. Дальнейшее сокращение рис. 143.

Парадокс картины выражен здесь в крайней форме. Но если картина «включена в саму себя», то молодой человек тоже включен сам в себя? На этот вопрос отвечает рис. 146.

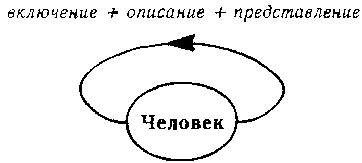
Рис. 146. Другой способ сокращения рис. 143.

Здесь мы видим молодого человека «внутри самого себя», в том смысле, какой получается от соединения трех аспектов «внутренности». Эта диаграмма напоминает нам о парадоксе Эпименида с его одноступенчатой автореференцией, в то время как двухступенчатая диаграмма похожа на пару утверждений, каждое из которых ссылается на другое. Затянуть Петлю туже не удается, но можно ее ослабить, вводя любое количество промежуточных уровней, таких как «рама картины», «аркада» и «здание». Сделав так, мы получим многоступенчатые Странные Петли, диаграммы которых изоморфны «Водопаду» (рис. 5) или «Спуску и подъему» (рис. 6) Количество ступеней определяется нашим чувством того, что «естественно», что может варьироваться в зависимости от контекста, цели, или нашего настроения. В конечном итоге, восприятие уровней — это вопрос интуиции и художественного вкуса.

Оказываются ли зрители, глядящие на «Картинную галерею,» затянутыми «в самих себя»? На самом деле, этого не происходит. Нам удается избежать этого водоворота благодаря тому, что мы находимся вне системы. Глядя на картину, мы видим то, что незаметно молодому человеку, — например, подпись Эшера «МСЕ» в центральном «слепом пятне». Хотя это пятно кажется дефектом, скорее всего, дефект заключается в наших ожиданиях, поскольку Эшер не мог бы закончить этот фрагмент картины без того, чтобы не вступить в противоречие с правилами, по которым он ее создавал. Центр водоворота остается — и должен оставаться — неполным. Эшер мог бы сделать его сколь угодно малым, но избавиться от него совсем он не мог. Таким образом мы, глядя снаружи, видим, что «Картинная галерея» неполна, чего молодой человек на картине заметить не в состоянии. Здесь Эшер дал художественную метафору Теоремы Геделя о неполноте. Поэтому Эшер и Гёдель так тесно переплетены в моей книге.